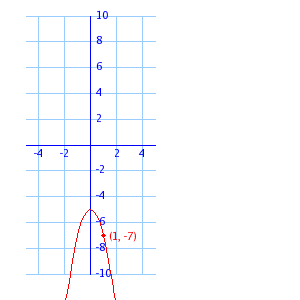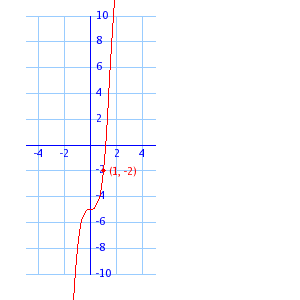If your child needs math practice, click here.
For sample problems, click here.
Here are some tips for Nonlinear Functions, which aligns with Florida state standards:
Nonlinear Functions
Linear functions are functions where x is raised only to the first power. On graphs, linear functions are always straight lines.
y = mx + b 3x + 5y - 10 = 0 y = 88x are all examples of linear equations.The graphs of nonlinear functions are not straight lines.
In this topic, we will be working with nonlinear functions with the form y = ax2 + b and y = ax3 b where a and b are integers.
Quadratic functions: y = ax2 + b
The graph of the function y = ax2 + b will look like a "U". This "U" shape graph is called a parabola. When a is positive, then the parabola opens up. When a is negative, then the parabola opens down.The highest or lowest point of parabolas is called the vertex. b determines where the vertex is on the graph. When b=0, the vertex is on the origin (0,0). When b = h where h is an integer, the vertex is on the point (0, h).
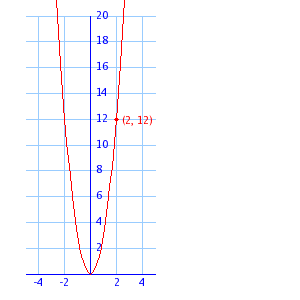In this graph, the vertex is the lowest point.
b = 0 because the vertex is on the origin.Use the point (2,12) to find a.
y = ax2 12 = a(2)2 12 = 4a 3 = a The equation is y = 3x.
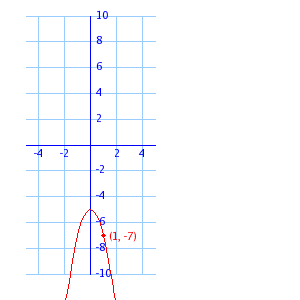In this graph, the vertex is the highest point.
b = -5 because the vertex is on (0, -5).Use the point (1, -7) to find a.
y = ax2 - 5 -7 = a(1)2 - 5 -7 = a - 5 -2 = a The equation is y = -2x - 5.
Cubic functions: y = ax3 + b
The graph of a cubic function has this shape
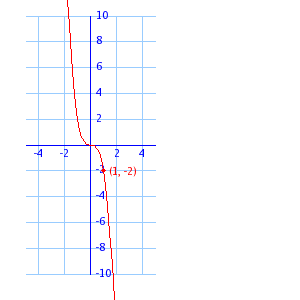b = 0 when the point of transition (from an upwards curve to a downwards curve) is on the origin (0,0).
This is an example of y = ax3 where a is negative.Use the point (1, -2) to find a.
y = ax3 -2 = a(1)3 -2 = a The equation is y = -2x3.
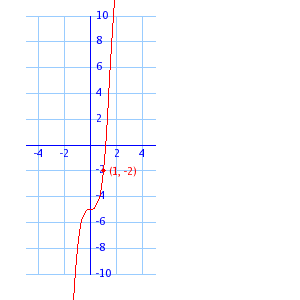b = -5 because the point of transition is on (0, -5). Use the point (1, -2) to find a.
y = ax3 - 5 -2 = a(1)3 - 5 -2 = a - 5 3 = a The equation is y = 3x3 - 5.
Copyright Accurate Learning Systems Corporation 2008.
MathScore is a registered trademark.
